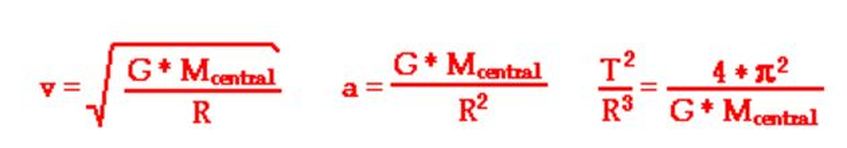|
Bell Work
1. Correct Kepler's Laws Worksheet. 2. Make a model with at least 3 planets (1 circular and 2 ellipses) going around a star. In your model, make sure to show and explain the following:
1. Take Satellite QUIZ 1 - LINK to THE QUIZ
2. Practice Calculating Satellite Motion Problems
3. Work on homework
|
Homework
Notes
Intervention |
Check Your Understanding
1. A satellite is orbiting the earth. Which of the following variables will affect the speed of the satellite?
a. mass of the satellite
b. height above the earth's surface
c. mass of the earth
Answer
2. Use the information below and the relationship above to calculate the T2/R3 ratio for the planets about the Sun, the moon about the Earth, and the moons of Saturn about the planet Saturn. The value of G is 6.67 x 10-11 N•m2/kg2.
SunM = 2.0 x 10^30 kg
EarthM = 6.0 x 10^24 kg
SaturnM = 5.7 x 10^26 kg
a. T2/R3 for planets about sun
b. T2/R3 for the moon about Earth
c. T2/R3 for moons about Saturn
3. One of Saturn's moons is named Mimas. The mean orbital distance of Mimas is 1.87 x 10^8 m. The mean orbital period of Mimas is approximately 23 hours (8.28x10^4 s). Use this information to estimate a mass for the planet Saturn.
See Answer
4. Consider a satellite which is in a low orbit about the Earth at an altitude of 220 km above Earth's surface. Determine the orbital speed of this satellite. Use the information given below.
G = 6.673 x 10-11 Nm2/kg2Mearth = 5.98 x 1024 kg
Rearth = 6.37 x 106 m
5. Suppose the ISS is in orbit about the earth at 400 km above its surface. Use the information given in the previous question to determine the orbital speed and the orbital period of the Space Shuttle.
See Answer
1. A satellite is orbiting the earth. Which of the following variables will affect the speed of the satellite?
a. mass of the satellite
b. height above the earth's surface
c. mass of the earth
Answer
2. Use the information below and the relationship above to calculate the T2/R3 ratio for the planets about the Sun, the moon about the Earth, and the moons of Saturn about the planet Saturn. The value of G is 6.67 x 10-11 N•m2/kg2.
SunM = 2.0 x 10^30 kg
EarthM = 6.0 x 10^24 kg
SaturnM = 5.7 x 10^26 kg
a. T2/R3 for planets about sun
b. T2/R3 for the moon about Earth
c. T2/R3 for moons about Saturn
3. One of Saturn's moons is named Mimas. The mean orbital distance of Mimas is 1.87 x 10^8 m. The mean orbital period of Mimas is approximately 23 hours (8.28x10^4 s). Use this information to estimate a mass for the planet Saturn.
See Answer
4. Consider a satellite which is in a low orbit about the Earth at an altitude of 220 km above Earth's surface. Determine the orbital speed of this satellite. Use the information given below.
G = 6.673 x 10-11 Nm2/kg2Mearth = 5.98 x 1024 kg
Rearth = 6.37 x 106 m
5. Suppose the ISS is in orbit about the earth at 400 km above its surface. Use the information given in the previous question to determine the orbital speed and the orbital period of the Space Shuttle.
See Answer
HOMEWORK
In a planetary system far away from our own galaxy, we find a series of 6 planets all having a kepler’s constant of 7.02E-15 sec^2/m^3
In a planetary system far away from our own galaxy, we find a series of 6 planets all having a kepler’s constant of 7.02E-15 sec^2/m^3
- 1. If we were able to watch one of the planets orbit their star and make one full revolution in 300 earth days (how many seconds?), what would be the distance from the center of the star to this planet? (Hint: Kepler's 3rd Law)
- 2. Based on the information in the last problem, calculate the mass of the star in the middle of this solar system? How does it compare to the sun? (The sun's mass is 1.98 EE 30 kg)
- 3. Another planet M85 within this same solar system has a mass of 5.2E+26 and a distance from the star of 5.3 E+13 meters. Calculate the velocity of how fast this planet revolves around the star.
- 4. How much acceleration does the star provide to the planet M85 in its orbit?
- 5. How many seconds does it take for M85 to orbit the star? Convert to Seconds